技术宅的力量：现阶段五行石合成最优方案

　　著名哲学家，佛学家，人类学家、逻辑学家，处女座形象代言人沙迦（シャカ/Syaka）曾经说过：“真相，是深不可测，却又非常美好的东西。遗憾的是，千百年以来，人类想要触摸真相却是非常困难的……”今天，我就为大家揭开五行石合成系统的神秘真相，与大家分享这一周以来我的发现和研究。

　　目前，比较流行的6级五行石的合成方法是用快速合成（系统自带）合成3级，再将3级合成4级，最后由4级转化为6级。这或许是一种比较好的方法，但是，这究竟是不是最省钱或者最省精力的方法呢？因为这个问题牵扯概率，我们不是狄阁老，没有判断推断果断的天赋。为了解决这个问题，我们必须通过计算才能找到答案。

　　首先，每合成一个石头都有消耗，我们的目的是用最少的消耗合成出一个6级石头。那么，如何来定义“消耗”呢？一般来讲，消耗(Consumption)分为金钱消耗和体力(stamina)消耗（是精力还是体力我也搞不清楚，就是右边那个槽）。由于金钱和体力同样具有价值，因此我们可以定义一个权重W，总消耗就等于

　　总消耗=W*金钱消耗+(1-W)*体力消耗 (1)

　　当W=0，我们可以找出消耗体力最少的方法；当W=1，我们可以找出消耗金最少的方法；如果综合考虑金币和体力消耗，就要找出最优的W。

　　其次，也是很重要很容易被忽视的一个问题，就是成功率(hit rate)。计算消耗时，成功率必须考虑在内。比如说，某一次合成显示消耗10金，消耗10点体力，成功率是50%，那么这个操作实际消耗就是20金+10点体力。因为从统计上来讲，只有一半的几率成功，另一半浪费掉了（我们暂且不考虑副产品）。所以，实际消耗是一个统计平均值(statistical average):（不知道什么是统计平均值的小喷油，请至【FAQ1】。不知道什么是概率的小盆友，请至【FAQ2】。）

　　实际消耗=显示消耗/成功率 (2)

　　由于成功率的限制，和合成方法变的不是那么容易直接被看出来，而是需要通过计算才能得出。比如说，一个很简单的问题，如下图：如何合成2级石头最省钱？一般情况下，很家凭直觉会选择第一种。但是实际上，假设1级五行石的单价是70银，那么第一种的金钱消耗是(70*4+12)/0.9436=3金9银45铜，第二种金钱消耗是(70*3+9)/0.7777=2金81银60铜。从统计上讲，明显第二种更省钱。因此，我所做的工作就是将所有可行的方法产生的消耗都计算一遍，从中挑出消耗最少的，当然这个工作要借助编程来完成。

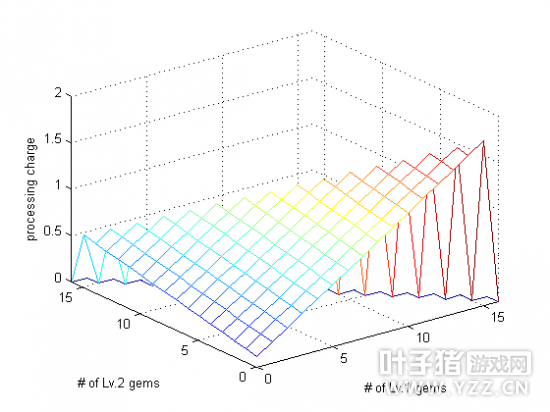
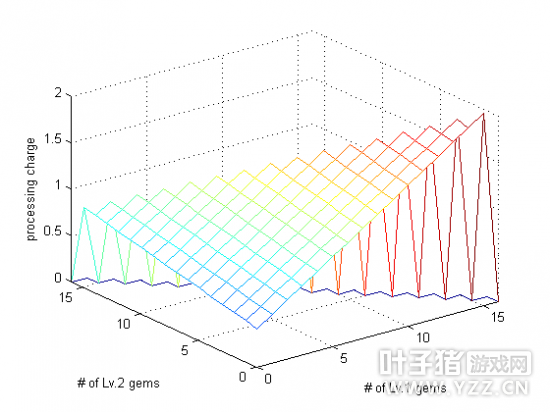
　　经计算，不考虑主石头（被合成的石头，放在上面槽里的那个）的放法，仅仅子石头从1级到5级就有20349种放法，因此逐个采样记录成功率和加工费是不可能的。所以，我对加工费和成功率做了一下研究，找到了这两个量变化的规律。

　　【加工费分析】

　　很多基三player往往不考虑加工费，觉得加工费就几金，可以忽略。实际上，每合成一个6级石头需要N次合成，每一次的加工费叠加起来足可以跟石头的价值相比拟，不可以忽略。不难发现，每添加一个同等级的石头，加工费的增长是线性的。（不知道什么是线性的小盆友，请至【FAQ3】。）一开始我曾经认为，不管主石头放的是几级，只要各个等级的子石头的数量确定了，加工费就是个定值。但不难发现，线性公式里面的常数项，也就是截距(intercept)，是跟随主石头等级变化的。根据我的研究，加工费用公式表示为（单位：金，下同）

　　加工费=5.6225*[5级石头的个数]+1.1596*[4级石头的个数]+0.4107*[3级石头的个数]+0.111*[2级石头的个数]+0.03*[1级石头的个数]+C (3)

　　where C=5.6225 if 主石头是5级；

　　C=1.1596 if 主石头是4级；

　　C=0.4107 if 主石头是3级；

　　C=0.111 if 主石头是2级；

　　C=0.03 if 主石头是1级。

　　显然，这个常数项C等于与主石头等级相同的子石头的个数的系数（斜率）。这个函数牵扯6个变量，是个6维平面，无法画图给大家看，不过，当子石头只有1级和2级的时候，主石头为2级或3级的加工费分布是一个3维的，如下图所示（左图为2级主石头，右图为3级主石头。因为是线性关系，所以是平面。因为主石头等级影响截距，所以两个平面高度不同）。

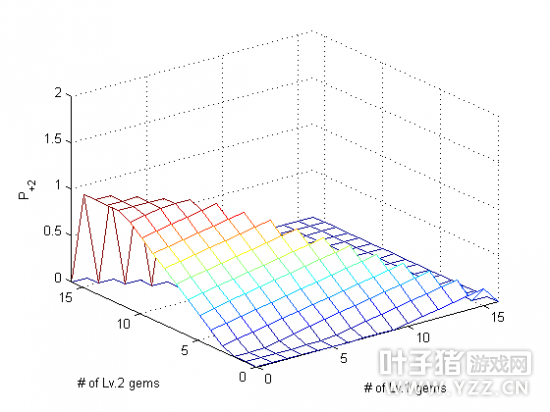
　　在这个图的后方有一个明显的断层，这是由于受到子石头个数的限制（constrains）。最多只能放16个子石头。

　　【概率分析】

　　成功率与加工费不一样，它不是取决于每一个等级子石头的数量，而是取决于与主石头等级相同的子石头的数量和比主石头等级低一级和两级的子石头的数量。主要注意的是，如果主石头是5级，概率分布情况稍有不同，我们分开讨论。另外，当所有的石头摆好以后，会有两个概率出现：升一级的成功率和升两级的成功率，我们也分开讨论。

　　先来看让主石头升一级的概率。当主石头不是5级时（5级主石头稍后讨论），大家会发现，当放的同一等级的石头越来越多，成功率就越接近1，但是超过一定的数量，成功率就会下降，这时候主石头升两级的成功率就会上升。我将这个变化趋势称为上升概率(ascendingprobability)和下降概率(descending probability)。经过实验计算，当主石头不为5级时，上升概率为

　　上升概率=0.3889*[与主石头等级相同的子石头的个数]+0.1089*[比主石头低一级的子石头的个数]+0.0304*[比主石头低两级的子石头的个数] (4)

　　比主石头低三级的子石头对合成不起任何作用。同样的方法，当主石头不为5级时，下降概率为

　　下降概率=-0.1089*[与主石头等级相同的子石头的个数]-0.0304*[比主石头低一级的子石头的个数]-0.0085*[比主石头低两级的子石头的个数]+1.2696 (5)

　　很明显，上升概率的系数和下降概率的系数错位相等。

　　再来看当主石头是5级石头的情况。这种情况下，没有下降概率，因为石头不能合成7级，不需要补偿升两级的概率。这时候，放2级石头对概率有影响，影响规律是

　　主石头是5级石头时的概率=0.3889*[与主石头等级相同(Lv.5)的子石头的个数]+0.1089*[比主石头低一级(Lv.4)的子石头的个数]+0.0304*[比主石头低两级(Lv.3)的子石头的个数]+0.0085*[比主石头低三级(Lv.2)的子石头的个数] (6)

　　再看主石头升两级的概率。这个概率只有上升阶段，而且是线性，与升一级的下降概率分布对称，并且与比主石头等级高一级的子石头数量有关：

　　升两级的概率=0.3889*[比主石头高一级的子石头的个数]+0.1089*[与主石头等级相同的子石头的个数]+0.0304*[比主石头低一级的子石头的个数]+0.0085*[比主石头低两级的子石头的个数]-0.2704 (7)

　　说的比较复杂，上个图就明白了

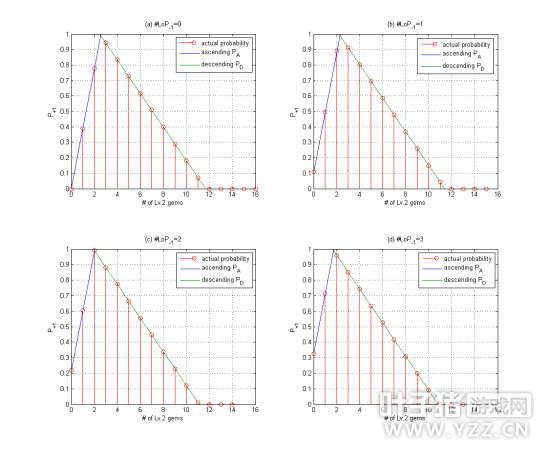
　　这个图是当主石头是2级的时候，升一级的概率。横轴代表2级子石头的个数，4个图分别放了0,1,2,3个1级子石头。可以看出来，每个三角形的形状完全一样，就是每两个之间有一个位移，而且是等量平移，这就说明在1级石头数量这个轴上也是线性。但是有一点不要忘记，不管概率怎么分布，概率的值必须大于等于0且小于等于1，如果上面的公式分布超出了这个范围，要把概率归为0或者1，如下图，在升两级的概率分布中，红色和紫色超出这个范围的部分被设置为1和0。